May 03, 2010 - By Charles Calkins, OCI Senior Software Engineer
Middleware News Brief (MNB) features news and technical information about Open Source middleware technologies.
Introduction
The OpenMP [1] specification describes a collection of compiler directives for marking regions of code for parallel execution and synchronization. These directives are expressed as pragmas in C/C++, and as comments in FORTRAN. A function-call-style API is also available which provides additional functionality.
The development of the OpenMP specification is under the purview of the OpenMP Architectural Review Board, a non-profit corporation whose members include HP, IBM, Intel, Sun Microsystems, Microsoft and others. Version 1.0 of the specification for FORTRAN was released in October 1997, and for C/C++ in October 1998. Version 3.0 of the specification, released in May 2008, is the most current as of this writing.
OpenMP is supported by a number of compilers [2], for both UNIX and Windows platforms. To demonstrate OpenMP's versatility, the code provided in this article has been tested with GCC 4.2.x (supporting OpenMP v3.0) and Visual Studio 2008 (supporting OpenMP 2.0), on 32-bit GNU/Linux, 64-bit GNU/Linux, and 32-bit Windows targets, respectively. Please see the sidebar at the end of the article for details.
As there are many OpenMP tutorials available online, such as [3] [4] [5], and in print, including [6] [7], we shall focus on the core capability of OpenMP — code block parallelization, specifically that of a for loop.
Block Parallelization
In C/C++, OpenMP directives begin as #pragma omp, followed by the desired operation. The API methods look like standard C function call, and require the inclusion of the omp.h header file.
The most important of the OpenMP directives is
#pragma omp parallelwhere the block of code following this directive will be executed in parallel. Multiple threads will be created to perform the work of the block, and the threads terminated when the block completes. The collection of threads created to execute a block is known as a team, where code execution proceeds as shown in the following diagram:

That is, a main thread is always executing but additional threads exist for the lifetime of the parallel block.
We shall now create our first OpenMP program, parallel_block1. The API method omp_get_num_threads() returns the number of threads currently executing. To invoke this method, omp.h must be included.
// parallel_block1.cpp
#include
#include
int main() {
std::cout << "Number of threads (outside parallel block): " <<
omp_get_num_threads() << std::endl;We mark a block of code for parallelization — at this point, a team of threads is started to execute the code within braces in parallel.
#pragma omp parallel
{Code marked with the master directive is only executed by the master thread, and by no other threads in the team.
#pragma omp master
std::cout << "Number of threads (inside parallel block): " <<
omp_get_num_threads() << std::endl;The barrier directive provides a point of synchronization between threads of the team — all threads of the team much reach that point before any thread in the team proceeds further.
#pragma omp barrierFinally, we execute a for loop. At each iteration of the loop, we print the rank of the currently executing thread in addition to the loop index. We use critical(lock_name) to execute the print statement inside of a critical section, to ensure that displayed output from one thread does not interleave the output of other threads. A critical section without a name acts as a global lock — only one can be executing in the program at any given time. A named critical section only serializes execution with other critical sections with the same name — critical sections with different names can still execute concurrently.
for (int i=0; i<16; i++)
{
#pragma omp critical(log)
std::cout << "<" << omp_get_thread_num() <<
":" << i << ">" << std::flush;
}
}
std::cout << std::endl;
return 0;
}Executing the above on a quad core Xeon (x86_64 GNU/Linux, each core running at 2.33GHz) produces the following output:
Number of threads (outside parallel block): 1
Number of threads (inside parallel block): 4
<2,0><1,0><2,1><1,1><0,0><2,2><3,0><0,1>
<3,1><0,2><3,2><0,3><3,3><0,4><3,4><0,5>
<3,5><2,3><1,2><2,4><1,3><2,5><3,6><2,6>
<1,4><0,6><3,7><1,5><2,7><3,8><0,7><3,9>
<0,8><3,10><0,9><3,11><0,10><3,12><2,8><1,6>
<2,9><1,7><2,10><1,8><2,11><1,9><2,12><1,10>
<2,13><1,11><2,14><1,12><2,15><1,13><0,11><1,14>
<0,12><1,15><0,13><3,13><0,14><3,14><0,15><3,15>Before the parallel directive, only one thread is executing, but after the directive, four threads are executing — unless indicated otherwise by directive, API method, or environment variable, one thread per processor will be created.
The output from the for loop is not as desired — it is not yet parallelized. Instead of dividing the loop across all threads, each thread executed its own complete loop. To divide a for loop across threads, one must use the for directive. We create parallel_block2, identical to the previous example, but with the for directive added just prior to the loop:
// parallel_block2.cpp
...
#pragma omp for
for (int i=0; i<16; i++)
{
...The code now executes as expected — the for loop is divided across the executing threads.
Number of threads (outside parallel block): 1
Number of threads (inside parallel block): 4
As parallelizing a for loop is a common operation, OpenMP allows the parallel and for keywords to be combined together, as in:
// parallel_for.cpp
#include
#include
int main() {
#pragma omp parallel for
for (int i=0; i<16; i++)
{
#pragma omp critical(log)
std::cout << "<" << omp_get_thread_num() << ":" <<
i << ">" << std::flush;
}
std::cout << std::endl;
return 0;
}Executing this produces the same assignment of loop indices to threads, as in the previous example.
<0:0><1:4><2:8><1:5><3:12><1:6><2:9><1:7>
<2:10><3:13><2:11><3:14><3:15><0:1><0:2><0:3>Other options can be used with the parallel directive, such as the schedule directive. Static scheduling is the default, where forloop indices are divided amongst threads by allocating the first (total_loop_iterations ÷ number_of_team_threads) number of iterations to the first thread, the same number to the second thread, etc., until all loop indices have been allocated. In the example above, the loop ran for 16 iterations, and 4 threads are members of the team, so 16 ÷ 4 = 4 loop indices are allocated to each thread. Thus, indices 0, 1, 2 and 3 were allocated to thread 0, indices 4, 5, 6 and 7 to thread 1, indices 8, 9, 10 and 11 to thread 2, and indices 12, 13, 14 and 15 to thread 3. Although this is sufficient in many cases, the following example will demonstrate that this is not always ideal.
We first define a helper function to put a thread to sleep for a given number of milliseconds:
// ms_sleep.cpp
#ifdef WIN32
#include
#else
#include
#endif
void ms_sleep(int ms) {
#ifdef WIN32
Sleep(ms);
#else
usleep(ms * 1000);
#endif
}For our example, we use the OpenMP API method omp_get_wtime() to provide a measure of execution time.
// parallel_for_static.cpp
#include
#include
#include "ms_sleep.h"
int main() {
double start = omp_get_wtime();Although it is the default, we specify schedule(static) for clarity, plus force OpenMP to form a team of two threads, regardless of the underlying architecture. As before, we print the assignment of thread rank to loop index.
#pragma omp parallel for schedule(static) num_threads(2)
for (int i=0; i<4; i++)
{
#pragma omp critical(log)
std::cout << "<" << omp_get_thread_num() << ":" <<
i << ">" << std::flush;Unlike before, however, the amount of work performed by each loop index varies. Indices 0 and 1 execute in five seconds, but indices 2 and 3 in half of a second.
if (i<2)
ms_sleep(5000); // simulate long work
else
ms_sleep(500); // simulate short work
}Lastly, we display the elapsed time.
double end = omp_get_wtime();
std::cout << std::endl << "Elapsed: " << end-start << std::endl;
return 0;
}Executing this example produces:
<0:0><1:2><1:3><0:1>
Elapsed: 10.0047
The static scheduling has allocated loop indices 0 and 1 to thread 0, and loop indices 2 and 3 to thread 1. Thread 0 has 10 seconds of work to complete, but thread 1 only one second. Thread 1 completes well before thread 0, and the total execution time is ten seconds.
Dynamic scheduling improves this behavior. Instead of preallocating loop indices to threads, dynamic scheduling allocates loop indices to threads as threads become available to perform work. Changing the directive to the following:
// parallel_for_dynamic.cpp
#pragma omp parallel for schedule(dynamic) num_threads(2)produces this execution:
<0:0><1:1><0:2><1:3>
Elapsed: 5.50504Initially, threads 0 and 1 are available for work. Thread 0 is assigned loop index 0, and thread 1 loop index 1. Both threads are now executing loop indices that take five seconds to complete, so both threads are ready for new work in five seconds. When they finish, they are assigned loop indices 2 and 3 which take half a second to complete, so the total execution time is five and a half seconds.
Case Study: Matrix Multiplication
A computation that can benefit from parallelization is matrix multiplication. Given matrix A with I rows and K columns, and matrix B with K rows and J columns, multiplication of A and B results in a matrix C with I rows and J columns, with the elements of Ccalculated as follows:
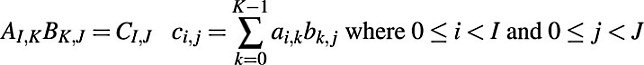
In order to demonstrate parallelization of matrix multiplication, we create a library, matrix, containing a number of helper classes and functions. The helpers are described below, but please see the code archive that accompanies this article for their full implementation.
class Matrix |
Has accessors Rows() and Cols() to return the matrix dimensions, and parenthesis operators to allow individual matrix components to be read and set. |
Clear(M) |
Set all components of the given matrix to zero. |
Fill(M) |
Assign deterministic values to all components of the given matrix. |
Identity(M) |
Assuming M is a square matrix, assign components of M such that M is an identity matrix. |
Compare(M1, M2) |
Return true if matrices M1 and M2 are identical, to ensure algorithm correctness. |
To demonstrate parallelism with OpenMP, we will create three implementations of the summation provided above.
Single-Threaded Implementation (mm_basic)
Implementing the summation is straightforward. We augment the matrix library with the following function in the file mm_basic.cpp:
// matrix/mm_basic.cpp
#include "matrix.h"
void mm_basic(const Matrix &a, const Matrix &b, Matrix &product) {
for (int i=0; i<a.Rows(); i++)
for (int j=0; j<b.Cols(); j++)
for (int k=0; k<a.Cols(); k++)
product(i,j) += a(i,k) * b(k,j);
}To benchmark this function, we create a project with the same name as the function, and allow the size of the matrix, n, to be supplied on the command-line, but defaulting to 50 if not specified:
// mm_basic/mm_basic.cpp
#include "matrix.h"
#include "mm_basic.h"
#include
#include
#include
int main(int argc,char *argv[]) {
int n = 50;
if (argc>1)
n = atoi(argv[1]);Next, we create two square matrices, I and A, with n rows and n columns. I is populated as an identity matrix, and A with specific values. We also create a matrix, product, initially zero, to contain the multiplication of I and A.
Matrix I(n,n);
Identity(I);
Matrix A(n,n);
Fill(A);
Matrix product(n,n);
Clear(product);We time the peformance of mm_basic() using the OpenMP timing methods that we used before and write the result to standard output.
double start = omp_get_wtime();
mm_basic(I,A,product);
double end = omp_get_wtime();
std::cout << n << " " << end-start << std::endl;Finally, we confirm that the multiplication was accurate to confirm that our algorithm executed correctly. As a matrix multiplied by an identity matrix is unchanged (the same as multiplying a scalar by 1), we know that product must be identical to A.
if (!Compare(A,product)) {
std::cout << "not equal" << std::endl;
return 1;
}
return 0;
}Parallelization with OpenMP (mm_basic_omp)
Parallelizing this algorithm with OpenMP is trivial — we only need to mark the outer for loop to run in parallel and leave the rest unchanged — this parallelizes the outer loop, allowing the inner loops to run concurrently over values of i. As the Matrix class allows concurrent writes to different matrix elements, we do not need to synchronize access to them. We create the function mm_basic_omp() in the file matrix_basic_omp.cpp and add it to the matrix library.
// matrix/matrix_basic_omp.cpp
#include "matrix.h"
void mm_basic_omp(const Matrix &a, const Matrix &b, Matrix &product) {
#pragma omp parallel for
for (int i=0; i<a.Rows(); i++)
for (int j=0; j<b.Cols(); j++)
for (int k=0; k<a.Cols(); k++)
product(i,j) += a(i,k) * b(k,j);
}We also create an application to benchmark this function, mm_basic_omp, identical to mm_basic as given above, but with mm_basic_omp() called to perform the multiplication.
Parallelization with ACE (mm_basic_ace)
Using ACE [8], this algorithm can be explicitly parallelized, but, as we shall see, OpenMP provides simpler, more readable code. We start by creating a structure to store thread parameters, such as references to the matrices to multiply and to the result. We want to perform the same work assignment as does OpenMP, so we also store a range of loop indices of the outer for loop (the loop over I) for a given thread to act upon.
// matrix/mm_basic_ace.cpp
#include "matrix.h"
#include <ace/Thread_Manager.h>
struct mm_thread_param {
const Matrix &a_;
const Matrix &b_;
Matrix &product_;
int iLow_;
int iHigh_;
mm_thread_param(const Matrix &a, const Matrix &b, Matrix &c, int iLow, int iHigh) :
a_(a), b_(b), product_(product), iLow_(iLow), iHigh_(iHigh) {}
};Next, we create a thread function that performs the multiplication itself, over the specified index range.
ACE_THR_FUNC_RETURN mm_thread(void *param) {
mm_thread_param *p = reinterpret_cast<mm_thread_param *>(param);
for (int i=p->iLow_; iiHigh_; i++)
for (int j=0; jb_.Cols(); j++)
for (int k=0; ka_.Cols(); k++)
p->product_(i,j) += p->a_(i,k) * p->b_(k,j);
delete p;
return 0;
}Finally, we create an ACE_Thread_Manager and spawn threads, providing the appropriate range of indices to each thread to operate upon.
void mm_basic_ace(const Matrix &a, const Matrix &b, Matrix &product, int nthread) {
ACE_Thread_Manager tm;
tm.open();
for (int t=0; t<nthread; t++)
tm.spawn(mm_thread,
new mm_thread_param(a, b, product,
t*a.Rows()/nthread, (t+1)*a.Rows()/nthread));
tm.wait();
tm.close();
}Results
The three tests described above are graphed below. For each data point, 6 runs on the quad core Xeon were performed, with the fastest and slowest times removed, and the remaining four runs averaged.
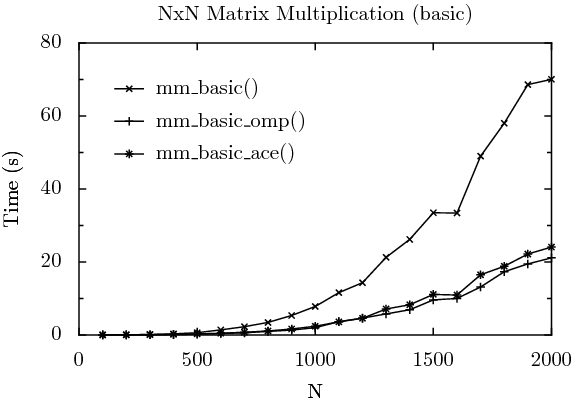
As expected, the single-threaded version of the algorithm, mm_basic() performed the slowest, taking 70.02 seconds to multiply a 2000x2000 matrix. The OpenMP version, mm_basic_omp(), was the fastest, at 21.11 seconds. The ACE version, mm_basic_ace(), was close, but the added overhead of hand-crafting the parallelization caused a small penalty to be incurred — it executed in 24.07 seconds. The faster execution, and simpler code (only one line to parallelize the basic algorithm for OpenMP, vs. many for ACE), demonstrates that OpenMP is worthy of consideration when algorithm parallelization is desired.
Be Cache-Friendly (mm_cache)
Although parallelization can often improve performance, one must not forget that using an improved algorithm can also be beneficial. Matthew Steele in [9] presents a modification of the basic matrix multiplication algorithm which improves cache locality, using a technique known as blocking. A variant of this algorithm is presented in [10], and [11] provides in-depth discussion of blocking. The benefits of cache locality are described in [10] and [12].
To test the improved algorithm, we create the method mm_cache() in mm_cache.cpp in the matrix library. We first provide a helper function, for convenience, so the caller only needs to provide the matrices and a threshold parameter.
// matrix/mm_cache.cpp
#include "matrix.h"
#include "mm_cache.h"
void mm_cache(const Matrix &a, const Matrix &b, Matrix &product, int threshold) {
mm_cache(a,b,product, 0,a.Rows(), 0,b.Cols(), 0,a.Cols(), threshold);
}The extension to the matrix multiplication algorithm is to only start multiplying ranges of the matrix when the amount of work to do is reduced to a block less than the size of the supplied threshold.
// the matrix dimensions as expressed here are a[i,k], b[k,j] and product[i,j]
void mm_cache(const Matrix &a, const Matrix &b, Matrix &product,
int i0, int i1, int j0, int j1, int k0, int k1, int threshold) {
int di = i1 - i0;
int dj = j1 - j0;
int dk = k1 - k0;
if (di >= dj && di >= dk && di >= threshold) {
int mi = i0 + di / 2;
mm_cache(a, b, product, i0, mi, j0, j1, k0, k1, threshold);
mm_cache(a, b, product, mi, i1, j0, j1, k0, k1, threshold);
} else if (dj >= dk && dj >= threshold) {
int mj = j0 + dj / 2;
mm_cache(a, b, product, i0, i1, j0, mj, k0, k1, threshold);
mm_cache(a, b, product, i0, i1, mj, j1, k0, k1, threshold);
} else if (dk >= threshold) {
int mk = k0 + dk / 2;
mm_cache(a, b, product, i0, i1, j0, j1, k0, mk, threshold);
mm_cache(a, b, product, i0, i1, j0, j1, mk, k1, threshold);
} else {
for (int i = i0; i < i1; i++)
for (int j = j0; j < j1; j++)
for (int k = k0; k < k1; k++)
product(i,j) += a(i,k) * b(k,j);
}
}There are two obvious ways to parallelize this version of the algorithm. The first, as mm_cache_omp1(), is to parallelize the multiplication loop itself, as we had done before with mm_basic().
// matrix/mm_cache_omp1.cpp
...
} else {
#pragma omp parallel for
for (int i = i0; i < i1; i++)
for (int j = j0; j < j1; j++)
for (int k = k0; k < k1; k++)
product(i,j) += a(i,k) * b(k,j);
}
...The second way, as mm_cache_omp2() to parallelize the cache-friendly version of the algorithm, is to create a thread for ranges of indices of the loop over I, as in mm_basic_ace(). We use the rank of the current thread, obtained from omp_get_thread_num(), to determine the range to calculate.
// matrix/mm_cache_omp2.cpp
#include "matrix.h"
#include "mm_cache_omp2.h"
#include "mm_cache.h"
#include
void mm_cache_omp2(const Matrix &a, const Matrix &b, Matrix &product, int threshold) {
#pragma omp parallel
{
int start = omp_get_thread_num()*a.Rows()/omp_get_num_threads();
int end = (omp_get_thread_num()+1)*a.Rows()/omp_get_num_threads();
mm_cache(a,b,product, start,end, 0,b.Cols(), 0,a.Cols(), threshold);
}
}Results
As before, we create test drivers to measure performance. The results are graphed below. Also as before, for each data point, six runs were made, the fastest and slowest dropped, and the remainder averaged. A threshold (blocking size) of 100 was used for the cache algorithm tests, which, experimentally, led to the best results on the architectures that were profiled. A more rigorous determination of a threshold value depends upon cache size and other factors, as discussed in [11].
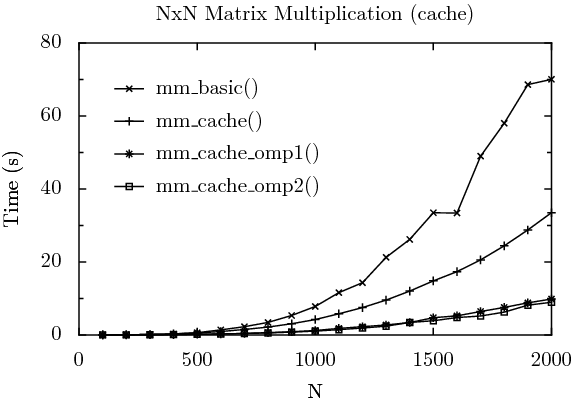
In this graph, mm_basic() is as before, executing in 70.02 seconds when multiplying a 2000x2000 matrix. The cache-friendly version of the algorithm, mm_cache(), still single-threaded, multiplies the same matrix in 33.49 seconds. This is more than twice as fast as the basic algorithm, with only cache locality taken into consideration to produce such a dramatic improvement. Parallelizing this version of the algorithm runs in 9.83 and 8.95 seconds, respectively, for mm_cache_omp1() and mm_cache_omp2(). Presumably mm_cache_omp2() is slightly faster than mm_cache_omp1() as the thread team is created once at the start of the algorithm, as opposed to having a thread team created and destroyed for each block that is multiplied. Note that 8.95 seconds is also more than twice as fast as the 21.11 seconds of the OpenMP parallelization of the basic algorithm — the cache-locality optimization also improves the parallized version of the algorithm by a comparable ratio as with the single-threaded one.
Conclusion
This article demonstrates that OpenMP is a viable technology to consider for algorithm parallelization, although improvements in algorithms themselves can also be of great benefit.
SIDEBAR
The code in this article has been tested under both 32-bit and 64-bit GNU/Linux with GCC 4.2.1 and 4.2.2, and 32-bit Windows XP and Vista with Visual Studio 2008. Compiling an application under GCC that uses OpenMP requires the -fopenmp compiler option. Similarly, Visual Studio requires the /openmp compiler option. The code in this article uses MPC to generate appropriate projects, encapsulating the OpenMP settings in the openmp.mpb base project, as follows:
// openmp.mpb
project {
specific(vc8,vc9,vc10) {
openmp = true
}
specific(make) {
genflags += -fopenmp
}
}If compiling with Visual Studio 2005 (vc8), Visual Studio 2008 (vc9), or Visual Studio 2010 (vc10), the openmp variable is enabled. If generating projects with make, implying GCC, -fopenmp is added to the compiler's command-line.
Data collected for the graphs is included in the code archive associated with this article. Latex was used for the equation formatting, and pyxplot for the graphs. Scripts for collecting data and generating the graphs are also included in the code archive.
References
[1] OpenMP home
http://openmp.org
[2] OpenMP Compilers
http://openmp.org/wp/openmp-compilers/
[3] Guide into OpenMP: Easy multithreading programming for C++
http://bisqwit.iki.fi/story/howto/openmp/
[4] OpenMP
https://computing.llnl.gov/tutorials/openMP/
[5] Introduction to OpenMP
http://heather.cs.ucdavis.edu/~matloff/openmp.html
[6] Chapman, Jost and van der Pas. Using OpenMP MIT Press, Cambridge, Massachusetts, 2007.
[7] Chandra, et. al. Parallel Programming in OpenMP Academic Press, San Diego, CA, 2001.
[8] ACE + TAO
https://objectcomputing.com/products/ace
[9] A Tale of Two Algorithms: Multithreading Matrix Multiplication
http://www.cilk.com/multicore-blog/bid/6248/A-Tale-of-Two-Algorithms-Multithreading-Matrix-Multiplication
[10] Locality of reference
http://en.wikipedia.org/wiki/Locality_of_reference
[11] Jin, Mellor-Crummey, Fowler Increasing Temporal Locality with Skewing and Recursive Blocking
http://www.sc2001.org/papers/pap.pap268.pdf
[12] Sutter Maximize Locality, Minimize Contention
http://www.drdobbs.com/architecture-and-design/208200273
