Pathfinding with A*

by Charles Calkins, Principal Software Engineer

October 2014

Introduction

A number of algorithms exist for finding paths in graphs, and a venerable one from 1968, useful in applications such as game development and robotics, is A*. This article describes the A* algorithm and graphically demonstrates paths that it finds.

A*

Given a graph of nodes connected by edges, the A* search algorithm finds a "least cost" path from a starting node to a destination node, along the edges that connect them. For a given node, the least cost path to it is maintained, and, at each iteration of the algorithm, the path with the current least cost is extended by evaluating nearby nodes, to see which of them can extend the path in the most optimal way. When evaluating a node to extend a path, a heuristic cost function is used, composed of a known cost to the node, plus a cost which estimates the distance to the destination node. As long as the heuristic is "admissible" - that is, it never overestimates the cost to the destination node - then an appropriate path will be found.

Eric Lippert, in his blog series, illustrated an implementation of A* in C# for arbitrary graphs. While finding the shortest path in a graph is an abstract concept, finding the shortest path on a map is much easier to visualize, and, indeed, A* is often used in tile-based video games for a computer player to direct units from one place on the game map to another. So, to demonstrate A* in a more entertaining way, we'll show how it can be used for finding paths in the style of an old-school fantasy adventure game.

The Map

A typical fantasy game of the Ultima era consists of a collection of tiles, often retangular or hexagonal in shape, forming a large map. Each tile can contain terrain, architectural or other features which affect how difficult it is for a player to move across it. The features of each tile are shown graphically, providing an environment that that user can move around in.

While some games provide a top-down view, we will show an isometric one, thanks to the availability of tile graphics provided under the Creative Commons license. In this particular tile set, each tile is 54x54 pixels in size, with pink (RGB 255,0,255) indicating a transparent area, allowing tiles to be overlaid atop one another. A grass tile, for example, is as follows:

In the AStar project, in the attached code archive, all of the tiles we need are in the Images directory, and we will add them as resources to the executable. This is easily done in the project's MPC file:

// AStar\AStar.mpc
Embedded_Resource_Files {
    Images\*.PNG
}

The tiles are loaded as Bitmap objects by opening each resource as a stream.

// AStar\MapRenderer.cs
static Bitmap LoadBitmap(string name)
{
    using (Stream file = Assembly.GetExecutingAssembly()
            .GetManifestResourceStream("AStar.Images." + name))
        return new Bitmap(Image.FromStream(file));
}

For proper blending, pixels colored pink must be converted to true transparency by setting the alpha channel of the pixel to zero. While this can be done before the images are added as resources, it is straightforward to do so after the bitmap has been loaded. While the GetPixel() and SetPixel() methodes of Bitmap can be used to read and write pixel values, it is faster to manipulate the image bits directly, provided unsafe code blocks are allowed in the project. It is important to note that the color channels for each pixel are in BGRA order, rather than RGBA. In the code below, if the RGB value matches what is supplied in the function arguments, then the alpha channel value is set to 0.

// AStar\MapRenderer.cs
static Bitmap MakeTransparent(Bitmap bmp, byte r, byte g, byte b)
{
    BitmapData data = bmp.LockBits(
        new Rectangle(0, 0, bmp.Width, bmp.Height),
            ImageLockMode.ReadOnly, bmp.PixelFormat);
    unsafe
    {
        for (int x = 0; x < data.Width; x++)
        {
            int i = x * 4;
            for (int y = 0; y < data.Height; y++)
            {
                byte* row = (byte*)data.Scan0 + (y * data.Stride);
                // BGRA order
                if ((row[i] == b) && 
                    (row[i + 1] == g) && 
                    (row[i + 2] == r))
                    row[i + 3] = 0;  // transparent
            }
        }
    }
    bmp.UnlockBits(data);
    return bmp;
}

Allowing unsafe code blocks is done in MPC using this syntax:

// AStar\AStar.mpc
specific {
    allowunsafeblocks = true
}

We can represent a map as two arrays of strings, the first for a base and the second for an overlay, where each character in a string represents a terrain feature. For instance, "G" represents grass, "R" a road, and "W" a wall, and an example encoding is below.

new string[] {      new string[] {
    "GGGGGGGGGG",          "          ",
    "GGGGGGGGGG",          "     R    ",
    "GGGGGGGGGG",          "   RRRRR  ",
    "GGGGGGGGGG",          "     R W  ",
    "GGGGGGGGGG",          "     R W  ",
    "GGGGGGGGGG",          " 1   R W 2",
    "GGGGGGGGGG",          "       W  ",
    "GGGGGGGGGG",          "   WWWWW  ",
    "GGGGGGGGGG",          "       W  ",
    "GGGGGGGGGG"           "          "
}                   }

Class Map contains both the base and overlay string arrays, and is drawn using the Render() method. The width and height of the map are determined by the number of characters in a string, and the number of strings in the base tile string array. A blank image, bmpMap, is created as the canvas for the fully rendered map, and tiles are drawn in a sequence allowing background tiles to be occluded by foreground ones, and map overlay features to be drawn on top of base map features.

// AStar\MapRenderer.cs
static public Bitmap Render(Map map, Pos[] path)
{
    int mapWidth = map.MapData[0].Length;
    int mapHeight = map.MapData.Length;
 
    Bitmap bmpMap = new Bitmap(
        tileWidth * mapWidth + tileWidth / 2,
        tileHeight * (mapHeight + 1));
    Graphics gMap = Graphics.FromImage((Image)bmpMap);
 
    int x, y, cx, cy, px, py, pcx, pcy;
 
    for (int i = 0; i < mapHeight; i++)
        for (int j = mapWidth - 1; j >= 0; j--)
        {
            MapToXY(mapHeight, i, j, out x, out y, out cx, out cy);
 
            using (Bitmap b = LoadTile(map.MapData, i, j))
                if (b != null) gMap.DrawImage(b, x, y);
 
            using (Bitmap b = LoadTile(map.OverlayData, i, j))
                if (b != null) gMap.DrawImage(b, x, y);
        }
 
    // ...path rendering not shown here
}

Coordinates for tiles are calculated based on an isometric mapping, where north is to the upper left. Although the tile images are 54x54 pixels, a tile size of 52x26 is used for rendering. A one pixel overlap ensures that no gaps are shown between tiles, and the tile image area is predominantly in the lower half of the tile, with the upper half used for larger features, such as mountains, that extend well above ground level.

// AStar\MapRenderer.cs
const int tileWidth = 52;
const int tileHeight = 26;
 
static void MapToXY(int mapHeight, int i, int j, 
    out int x, out int y, out int cx, out int cy)
{
    x = (j * tileWidth / 2) + (i * tileWidth / 2);
    y = (i * tileHeight / 2) - (j * tileHeight / 2) + 
        ((mapHeight - 1) * tileHeight / 2);
    cx = x + tileWidth / 2;
    cy = y + tileHeight + tileHeight / 2;
}

The specific image to render for a given tile is determined within the LoadTile() method. Some tiles, such as grass or snow tiles, can be rendered without regard to neighboring tiles, so only one tile image is needed to represent them. Other features, such as roads and walls, must be drawn based on the content of neighboring tiles, so require one out of many images to be selected.

For example, consider a road tile that is to be rendered, where road tiles are also to the east and west of it. The image to select for the tile must be of a road that runs from east to west, connecting the neighboring road segments. If there was also a road tile to the north of it, than rather than an east to west road tile image, the appropriate image to select would be that of a T-junction, connecting the east, west and north road segments.

Calling the Neighbor() method for each of the cardinal directions builds a string containing the letters N, S, E and W, based on whether the position of the neighbor under consideration is within the bounds of the map, and the tile in the corresponding direction is of the same type as the tile being rendered.

// AStar\MapRenderer.cs
static string Neighbor(string[] map, char dir, int y, int x)
{
    char current = map[y][x];
    if (dir == 'N') y = y - 1;
    if (dir == 'S') y = y + 1;
    if (dir == 'W') x = x - 1;
    if (dir == 'E') x = x + 1;
    if ((y >= 0) && (y < map.Length) && (x >= 0) && (x < map[y].Length))
        if (map[y][x] == current)
            return dir.ToString();
    return string.Empty;
}
 
static Bitmap LoadTile(string[] map, int y, int x)
{
    string name = string.Empty;
    char current = map[y][x];
    string suffix =
        Neighbor(map, 'N', y, x) +
        Neighbor(map, 'E', y, x) +
        Neighbor(map, 'S', y, x) +
        Neighbor(map, 'W', y, x);

The string built by the calls to Neighbor() is used as a suffix of the image name. For the example above, the east to west road tile would have a suffix of EW, while the T-junction would have a suffix of NEW. Tiles of the tile set were renamed for consistency to follow this pattern.

The image name suffix is used as needed. As mentioned previously, as grass and snow can be represented by just one tile each (L1_Terrain001.PNG and L1_Terrain035.PNG), the suffix is not necessary.

Appropriate road and wall tiles must be selected from a set of tiles, however. For the above road examples, the east-west road L2_RoadDirtEW.PNG and the T-junction L2_RoadDirtNEW.PNG are required.

Incidentally, this tile set has a naming convention where a tile's layer is identified by the first characters of the tile image: L1_, L2_ or L3_. A tile with a higher layer number is designed to be overlaid on top of a tile with a lower layer number, such as a road tile (layer 2) on a grass or snow tile (layer 1).

The tile selection is performed by a list of if statements.

if (current == 'G')
        name = "L1_Terrain001";
 
    if (current == 'S')
        name = "L1_Terrain035";
 
    if (current == 'R')
        name = "L2_RoadDirt" + suffix;
 
    if (current == 'W')
        name = "L2_WallStone" + suffix;     
 
//  and more tile selections...

Lastly, the bitmap is made transparent, and returned to the Render() method which called it. The bitmap that is returned is drawn on the main map canvas via the call to gMap.DrawImage().

 if (!string.IsNullOrEmpty(name))
        return MakeTransparent(LoadBitmap(name + ".PNG"), 255, 0, 255);
 
    return null;
}

For the map defined by the base and overlay strings shown previously, the process above produces:

Pathfinding

On this map, we wish to find the lowest-cost path from the tent to the castle, taking into consideration features of the terrain. We shall consider grass as having a cost of 1 to move across, snow a cost of 3 to move across, a road reducing the cost of whatever it is over by 1/2 (so a road, on grass, has a cost of 1/2), and walls being impassable. We will also allow movement in the cardinal directions (N,S,E, and W), as well as diagonal movement (NE, SE, NW and SW).

Applying Lippert's algorithm to our 2-D map yields the following:

// AStar\AStar.cs
public Pos[] FindPath(Pos startPos, Pos destinationPos)
{
    var start = new Node(this, startPos.X, startPos.Y);
    var destination = new Node(this, destinationPos.X, destinationPos.Y);
    var closed = new HashSet<Node>();
    var open = new PriorityQueue<double, Path>();
    open.Enqueue(0, new Path(start));
    while (!open.IsEmpty)
    {
        var path = open.Dequeue();
        if (closed.Contains(path.LastStep))
            continue;
        if (path.LastStep.Equals(destination))
            return path.Select(node => 
                new Pos(node.X, node.Y)).ToArray();
        closed.Add(path.LastStep);
        foreach (Node n in path.LastStep.Neighbours)
        {
            double d = NeighborDistance(path.LastStep, n);
            var newPath = path.AddStep(n, d);
            open.Enqueue(newPath.TotalCost + 
                EstimatedDistance(n, destination), newPath);
        }
    }
    return null;
}

A Node represents a tile on the map, and a Path is a sequence of zero or more Nodes which maintains the order of traversal. If the last Node in a Path is the destination node, then the coordinates of the path are returned to the caller.

The A* algorithm is based on two collections. The first is the open list, a collection of partial Paths that have been explored, ordered by the path length, so obtaining the lowest cost partial path currently known is a fast operation. The second is the closed list, a collection of Nodes that have already been examined. Initially, the open list contains a Pathcontaining only the starting position, and the closed list is empty.

The algorithm proceeds as follows:

As long as the open list contains paths yet to explore, select the currently known path with the lowest cost.
If the last Node of the path has already been examined (it is found on the closed list), then select a new path to explore, or if it is the destination, then return the path as the best path that was found from the start to the destination.
Otherwise, mark the last Node of the path as examined (add it to the closed list), and add a number of new paths to the open list, where each path added is the existing path plus one of the neighbors of the Node. A Node is considered a neighbor if it is adjacent to the Node being examined (its X or Y coordinate differs by 1), and the terrain of the neighbor allows movement on to it (for example, if it is not a wall).

So, for this map, there are eight neighboring grass tiles of the tent tile that do not contain impassable features, so in the first iteration of the algorithm, eight new paths are added to the open list to explore.

When a Path is added to the open list, a cost function is computed for it, which consists of the known cost of the path so far, plus an estimate to the goal. Here, NeighborDistance() reflects the terrain features, and EstimatedDistance() is the Euclidian distance to the goal, to ensure that the cost is not overestimated. For a standard map, implemented by class StandardMap, the neighbor cost is calculated as:

// AStar\Main.cs
protected override double Distance(Node n1, Node n2)
{
    // cost is interpreted as the terrain cost 
    // of the square being moved on to
    char m = MapData[n2.Y][n2.X];
    char o = OverlayData[n2.Y][n2.X];
 
    // Grass=1, Snow=3
    // Road reduces the cost by 1/2
    double distance = 1.0;
    if (m == 'S')
        distance = 3.0;
    if (o == 'R')
        distance /= 2.0;
 
    // if both X and Y change, then moving in a diagonal,
    // so the distance is greater
    if ((n1.X != n2.X) && (n1.Y != n2.Y))
        distance *= 1.414;
 
    return distance;
}

Executing the above finds this path:

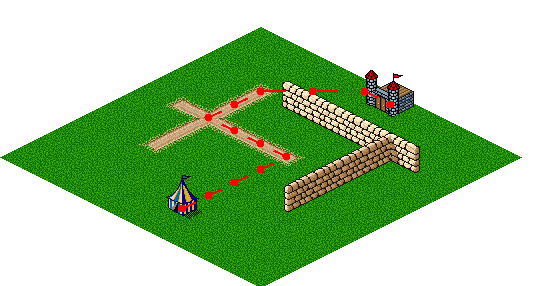
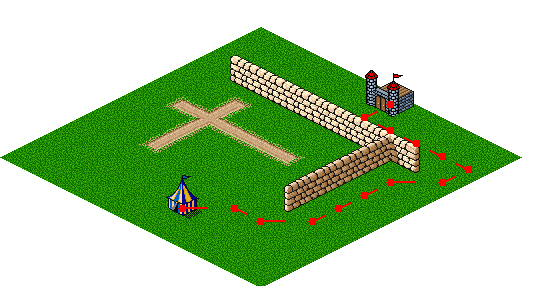
As expected, the A* algorithm determines that following the road as much as possible produces the lowest-cost path. If the wall is extended slightly, however, even the reduced cost of the road does not compensate for the extra distance.

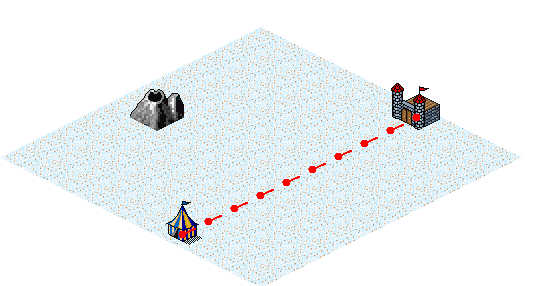
The cost function can be manipulated in many ways. Consider the desire for the "warmest path" when walking in snow. If the temperature is constant, then the path from the tent to the castle is a straight line, corresponding to the shortest distance between the two locations.

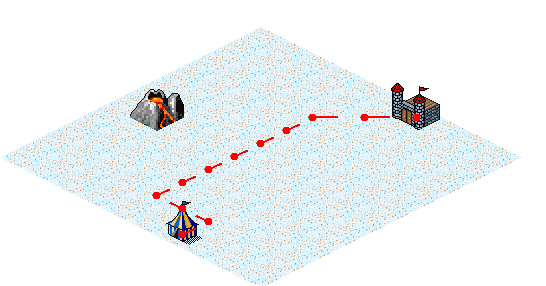
Suppose the volcano erupts, which increases the ambient temperature in the vicinity of the volcano. The path found now bends toward the volcano, in a compromise between travelling farther and being warm.

The cost function for the above looks like the following, where a lowercase "v" in the map definition string array represents a dormant volcano, and an uppercase "V" represents an erupting one:

// AStar\Main.cs
class VolcanoMap : StandardMap
{
    public VolcanoMap(string[] mapData, string[] overlayData) : 
        base(mapData, overlayData) { }
 
    protected override double Distance(Node n1, Node n2)
    {
        double distance = base.Distance(n1, n2);
 
        for (int j = 0; j < OverlayData.Length; j++)
            for (int i = 0; i < OverlayData[0].Length; i++)
                if (OverlayData[j][i] == 'V')
                {
                    double dV = Math.Sqrt(((i - n2.X) * (i - n2.X)) + 
                        ((j - n2.Y) * (j - n2.Y)));
                    if (dV <= 4.5)
                        distance /= ((5.0-dV)*2.0);
                }
 
        return distance;
    }
}

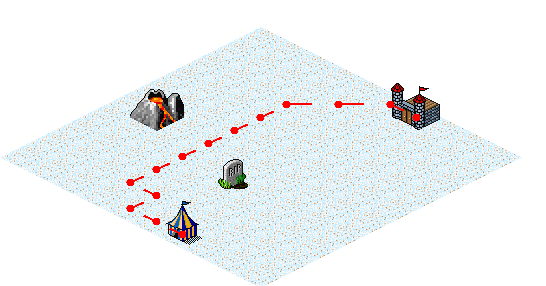
The cost function can also be manipulated to produce repulsive as well as attractive features. The desire to stay away from a tombstone generates a path to the south. The stairstep in the path is likely due to the hard effect cutoff at a distance of 2.5 from the tombstone. The effect of the tombstone isn't experienced until a move is made within its radius, which then results in the next step of the path moving back out of the affected area again.

A lowercase "t" in the map definition indicates a tombstone, and its repulsive effect can be produced as follows:

// AStar\Main.cs
class VolcanoTombstoneMap : VolcanoMap
{
    public VolcanoTombstoneMap(string[] mapData, string[] overlayData) : 
        base(mapData, overlayData) { }
 
    protected override double Distance(Node n1, Node n2)
    {
        double distance = base.Distance(n1, n2);
 
        for (int j = 0; j < OverlayData.Length; j++)
            for (int i = 0; i < OverlayData[0].Length; i++)
                if (OverlayData[j][i] == 't')
                {
                    double dV = Math.Sqrt(((i - n2.X) * (i - n2.X)) + 
                        ((j - n2.Y) * (j - n2.Y)));
                    if (dV <= 2.5)
                        distance *= (((3.0 - dV)+0.5)*1.1);
                }
 
        return distance;
    }
}

The path with an erupting volcano and a tombstone is even closer to the volcano than with the volcano alone, where the desire to stay away from the tombstone contributes to the added path distance.

Summary

The A* algorithm is straightfoward to implement, yet is very useful in finding paths in a variety of scenarios. Originally designed for robot navigation, examples of its use range from route planning to natural language parsing. It also has been shown to often perform better than other search algorithms, such as Dijkstra's Algorithm or Greedy Best-First-Search.

References

[1] A* search algorithm
http://en.wikipedia.org/wiki/A*_search_algorithm
[2] Path Finding Using A* in C# 3.0, Part One
http://blogs.msdn.com/b/ericlippert/archive/2007/10/02/path-finding-using-a-in-c-3-0.aspx
[3] Path Finding Using A* in C# 3.0, Part Two
http://blogs.msdn.com/b/ericlippert/archive/2007/10/04/path-finding-using-a-in-c-3-0-part-two.aspx
[4] Path Finding Using A* in C# 3.0, Part Three
http://blogs.msdn.com/b/ericlippert/archive/2007/10/04/path-finding-using-a-in-c-3-0-part-three.aspx
[5] Path Finding Using A* in C# 3.0, Part Four
http://blogs.msdn.com/b/ericlippert/archive/2007/10/04/path-finding-using-a-in-c-3-0-part-four.aspx
[6] Ultima I screenshot
http://en.wikipedia.org/wiki/Ultima_I:_The_First_Age_of_Darkness#mediaviewer/File:Ultima1-3.gif
[7] Dungeon Odissey Terrain Tiles library
http://pousse.rapiere.free.fr/tome/tiles/DO/tome-doterraintiles.htm
[8] MPC (The Makefile, Project, and Workspace Creator)
http://ociweb.com/products/mpc
[9] How to load PNGs and export to TGA keeping alpha in C#?
http://stackoverflow.com/questions/1514846/how-to-load-pngs-and-export-to-tga-keeping-alpha-in-c
[10] Drawing Isometric game worlds
http://stackoverflow.com/questions/892811/drawing-isometric-game-worlds
[11] Introduction to A*
http://theory.stanford.edu/~amitp/GameProgramming/AStarComparison.html

Software Engineering Tech Trends (SETT) is a regular publication featuring emerging trends in software engineering.