Performance Optimization on Modern Processor Architecture through Vectorization
By Yong Fu, OCI Software Engineer
December 2016
Introduction
Hardware provides performance through three sources of parallelism at different levels: thread parallelism, instruction level parallelism, and data parallelism.
Thread parallelism is achieved by splitting the workload equally, if possible, among threads.
Instruction level parallelism is achieved by applying the same operation to a block of code and by compiling into tight machine code.
Data parallelism is achieved by implementing operations to use SIMD (Single Instruction Multiple Data) instructions effectively.
Modern processors have evolved on all sources of parallelism, featuring massively superscalar pipelines, out-of-order execution, simultaneous multithreading (SMT) and advanced SIMD capabilities, all integrated on multiple cores per processor. In this article, we focus on optimizing performance through SIMD.
SIMD processing exploits data-level parallelism. Data-level parallelism means that the operations required to transform a set of vector elements can be performed on all elements of the vector at the same time. That is, a single instruction can be applied to multiple data elements in parallel.
All mainstream processors today such as Intel Sandy/Ivy Bridge, Haswell/Broadwell, AMD Bulldozer, ARM, and PowerPC implement SIMD features, although the implementation details may vary. Since most SIMD instructions on specific hardware involve operations of vector operands, sometimes SIMD operations are also referred to as vectorizations. Although there is a subtle difference between these two terms, in this article we use them interchangeably.
Intel Xeon Phi Architecture & Micro-Architecture for each Tile
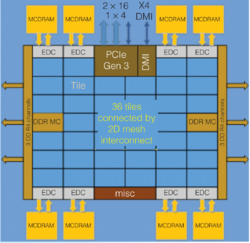
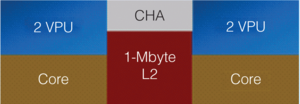
As an example of a processor with SIMD support, the above figure is an architecture diagram of Intel's Xeon Phi. In each core of Xeon Phi's 36 twin-core tiles there two vector processing units (VPUs) which provide the capability of two vector operations per cycle. To enhance vector operations fully exploiting VPUs, Knights Landing provides the AVX512 instruction set for operations on 512-bit vectors.
Vectorization
Vectorization or SIMD is a class of parallel computers in Flynn's taxonomy, which refers to computers with multiple processing elements that perform the same operation on multiple data points simultaneously. Such machines exploit data parallelism rather than concurrency since there are simultaneous computations, but only a single process at a given moment.
Single Instruction, Multiple Data (SIMD)
Scalar vs. SIMD Operation
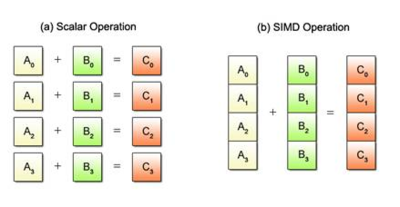
As shown in the figures above, unlike normal operations in which are the scalar operands, a vector operand SIMD operation is an operand containing a set of data elements packed into a one-dimensional array. The elements can be integer, floating-point, or other data types.
Automatic vectorization by compiler
Modern compilers like GCC can automatically identify opportunities and vectorize the code without interference by programmers. Automatic vectorization is straightforward and easy to perform with only the knowledge of related compiler options. However, automatic vectorization can only happen if memory is allocated totally and continuous and there are no data dependencies to prevent vectorization.
In addition, compilers don’t always have enough static information to know what they can vectorize. In some cases, they cannot achieve the same performance speedup as code optimized by a human expert.
Explicit vectorization
Besides automatic vectorization by compiler, the programmer may want to explicitly specify parallelism in the code. Vectorization may be explicitly exploited through the use of machine instructions (assembly language) or, to lower efforts of programmers, intrinsics which are functions directly wrapped low-level machine instructions and operations on vector data types.
There are also alternatives which provide higher abstractions than intrinsics. For example, a C++ library libsimdpp is a portable header-only library wrapping intrinsics and presents a single interface over several instruction sets. Boost.SIMD also offers a portable library for SIMD operation under the framework of Boost (currently it is a Boost candidate).
In addition, OpenMP and Open Computing Language (OpenCL) exploit both coarse-grained (thread) and fine grain parallelism (vectorization) in code. They are suitable for to applications exploiting large quantities of data parallelism on many-core architectures.
Generally, there are two places in code where vectorization could weigh in:
- Loop-based vectorization
- Traditionally, loop-based vectorization is the main focus of performance optimization through vectors. Loop-based vectorization can extract data parallelism from nested loops with large iteration spaces by loop transformations and by dependency analysis. There are many transformations that may need to be performed to allow the compiler to successfully exploit SIMD parallelism. These transformations include loop interchange, loop peeling, etc. Combining these transformations may generate better results than using one of them exclusively. The loop based vectorization techniques can be used to expose parallelism that can be exploited with a basic block vectorization algorithm, so the techniques can be complementary to each other.
- Basic block vectorization
- Since modern processors offer machine level operations which have smaller vector sizes than vector processor (a dedicated architecture for vector operations) and support a multitude of packing operations, a concept called Superword Level Parallelism (SLP) is introduced. SLP aims to exploit data level parallelism at a basic block level rather than only for loops. A basic block is a sequence of code without any control flow, where if the first statement executes in a block, if the block has no control flow, then all the others are guaranteed to execute as well. To create the appropriate SIMD instructions, SLP packs together isomorphic operations. Basic block level techniques are very effective in exploiting data parallelism in scalar operations. SLP can be exploited even in the presence of control flow. The basic idea is to convert if control to predicated instructions and SLP can be applied.
Vectorization Principles
For loop-based vectorization, there are some principles which can be applied strategically to vectorize the loop computation.
Identify the most important loops
Important loops can most easily be identified by its runtime via performance profiling tools like gprof. But if profiling is insufficient, it is possible to manually instrument some measurement code to provide more precise information. Normally those loops which execute for thousands or millions of iterations and run for very long times are likely candidates for vectorization. Given collected runtime information, one should only choose loops with most runtime and by optimizing them that desired speedup could be achieved. Other loops, in particular, those which are not parallel or otherwise difficult to optimize, may be ignored. So we do not need to waste efforts unnecessarily on those difficult codes.
Analyze loop dependencies
Loop dependencies are interleaved data operations which can prevent some loops from being parallelized. For example, consider the following example which repeatedly computes partial derivative of a 2-dimensional matrix:
Loop Dependencies
- for (int t = 0; t < l; ++t) {
- for (int i = 0; i < n; ++i) {
- for (int j = 0; j < n; ++j) {
- a[t+1, i, j] = a[t,i+1,j+1] + a[t,i-1,j-1] -
- a[t,i-1,j+1] - a[t,i+1,j-1]
- }
- }
- }
Obviously, the result of each step in the most inner loop depends on its neighbors of the previous steps which are controlled by outer loops. So the t loop and i loop cannot be computed in parallel. However, neither the i nor j loop carry any dependencies, and both can be vectorized.
Determine useful loop transformations
Normally, after identifying important loops and confirming the loops with vectorization after dependency analysis, there is a list of common transformations techniques for applying. The following transformations are only a small set, so programmers may need to explore more for specific situations.
- Stripmining. For a loop with a loop control variable
iincremented with some constant value X, stripmining creates inside this loop a new loop with control variable i2, increments i2 by X/Y and iterates Y times. The new loop is referred to as the strip loop, and the original loop is referred to as the control loop. This transformation does not in itself change the execution order of statements but code makes vectorization easy, and it does not change the iteration order so not to cannot violate dependencies. It does, however, introduce some added loop overhead.
Original Loop
- for (int i = 0; i < n; ++i) {
- x[i] = y[i] ;
- }
Loop After Stripmining
- for (int i = 0; i < n; i += 4) {
- for (int j = 0; (j < 4) && (i + j < n); ++j) {
- x[j] = y[j];
- }
- }
Now the inner loop can apply vectorization with vector operands size of 16 bytes (strictly speaking this example is only conceptual and needs more transformation to remove the condition j < 4 in inner loop guard before vectorization). Note that we also can use the technique of loop fission (described below) to split the original loop into two loops. One is transformed by stripmining and another is not.
- Unrolling. After a loop has been stripmined, it can be unrolled to increase the degree of instruction level parallelism and to allow basic block level vectorization. The unroll transformation merges the loop bodies of several iterations into a single body, removing some of the overhead of iterating through the loop. The number of merged iterations is called the unroll factor.
Loop After Unrolling
- for (int i = 0; i < n; i += 4) {
- if (i + 3 < n){
- x[i+0] = y[i+0];
- x[i+1] = y[i+1];
- x[i+2] = y[i+2];
- x[i+3] = y[i+3];
- } else {
- for (int j = 0 ; i + j < n; ++j) {
- x[i+j] = y[i+j] ;
- }
- }
Note that the example introduces an if statement when unrolling, which often causes a performance penalty. A more delicate algorithm using conditional variables could overcome this overhead.
- Fission. Fission refers to splitting a single loop into two or more loops. This transformation may enable vectorization by breaking inter-loop dependencies.
Loop After Fission
- for (int i = 0; i < (n - n%4); i += 4) {
- for (j = 0; j < 4; ++j) {
- x[j] = y[j];
- }
- }
- for (int k = (n - n%4); k < n; ++k) {
- x[k] = y[k];
- }
The example also uses loop stripmining. Compared to loop unrolling, this transformation adds more loops so it may add extra computation overhead.
In very rare cases only one or two transformations are used for vectorization. Generally, combinations of loop transformations can achieve better performance.
Vectorization with Intel AVX
In 2008, Intel introduced a new set of high-performance vectorization instructions called Advanced Vector Extensions (AVX). These instructions extend previous SIMD offerings, MMX instructions and Intel Streaming SIMD Extensions (SSE), by operating on larger chunks of data faster. Recently, Intel has released additional vectorization instructions in AVX2 and AVX512.
Intel SIMD Evolution
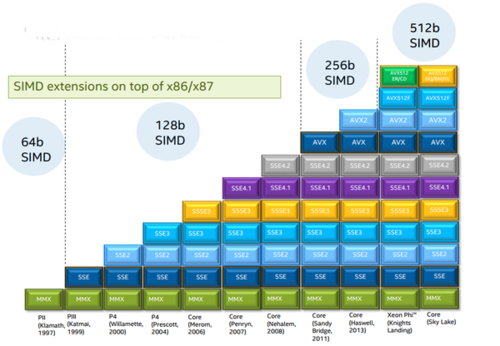
Since AVX/AVX2/AVX512 instruction sets include different SIMD functions, the first thing for vectorization with AVX is to check availability and support in the development and production environment. For example, on Linux the following command directly shows which AVX instruction set is supported on your platform.
cat /proc/cpuinfoFor example, on a Intel Core i7 (Sandy Bridge), the above command generate output like:
flags: ... sse4_1 sse4_2 x2apic popcnt tsc_deadline_timer aes xsave avx f16c rdrand ...The only relevant flag avx indicates that no more than basic avx operations are supported on this platform.
Intrinsics
Intel AVX is a low-level instruction set. To take advantage of AVX to speed up performance, one could inline a couple of assembly instructions. But obviously, this method is both non-portable and error-prone.
The preferred approach is to use intrinsics instead.
Simply speaking, intrinsics are functions that provide functionality equivalent to a few lines of assembly. Hence, the assembly version can serve as a drop-in replacement for the function at compile-time. This allows performance-critical assembly code to be inlined without sacrificing the beauty and readability of the high-level language syntax. At the same time, the correct intrinsics libraries for AVX development can be detected by following code snippet.
- #if defined(_MSC_VER)
- /* Microsoft C/C++-compatible compiler */
- #include <intrin.h>
- #elif defined(__GNUC__) && (defined(__x86_64__) || defined(__i386__))
- /* GCC-compatible compiler, targeting x86/x86-64 */
- #include <x86intrin.h>
- #elif defined(__GNUC__) && defined(__ARM_NEON__)
- /* GCC-compatible compiler, targeting ARM with NEON */
- #include <arm_neon.h>
- #elif defined(__GNUC__) && defined(__IWMMXT__)
- /* GCC-compatible compiler, targeting ARM with WMMX */
- #include <mmintrin.h>
- #endif
Data Types
In the intrinsic library, each data type starts with two underscores, an m, the width of the vector in bits, and real data type it builds. AVX512 supports 512-bit vector types that start with __m512, but AVX/AVX2 vectors don't go beyond 256 bits.
Data Types for AVX Intrinsics
| Data Type | Description |
|---|---|
__m128 |
128-bit vector containing 4 floats |
__m128d |
128-bit vector containing 2 doubles |
__m128i |
128-bit vector containing integers |
__m256 |
256-bit vector containing 8 floats |
__m256d |
256-bit vector containing 4 doubles |
__m256i |
256-bit vector containing integers |
If a vector type ends in d, it contains doubles, and if it doesn't have a suffix, it contains floats. It might look like _m128i and _m256i vectors must contain ints, but this isn't the case. An integer vector type can contain any type of integer, from chars to shorts to unsigned long longs. That is, an _m256i may contain 32 chars, 16 shorts, 8 ints, or 4 longs. These integers can be signed or unsigned.
Functions
The names of AVX/AVX2 intrinsics can be confusing at first, but the naming convention is really straightforward. Once you understand it, you'll be able to determine what a function does by looking at its name. A generic AVX/AVX2 intrinsic function is given as follows:
_mm<bit_width>_<name>_<vector_type>- bit_width. the size of the vector returned by the function. For 128-bit vectors, this is empty. For 256-bit vectors, this is
256. - name. the operation performed by the intrinsic
- vector_type. the data type contained in the function's primary argument vector
Vector type in function names actually refers to the type of data packed in the vector.
Vector Type of AVX Intrinsics Functions
| Vector Type | Description |
|---|---|
ps |
floats (ps stands for packed single-precision) |
pd |
doubles (pd stands for packed double-precision) |
epi8/16/32/64 |
8-bit/16-bit/32-bit/64-bit signed integers |
epu8/16/32/64 |
8-bit/16-bit/32-bit/64-bit unsigned integers |
si128/256 |
unspecified 128-bit vector or 256-bit vector and could be any type |
m128/m256<i/d> |
identifies input vector types when types when they're different than the type of the returned vector |
As an example, consider _mm256_srlv_epi64. Even if you don't know what srlv means, the _mm256 prefix tells you the function returns a 256-bit vector, and the _epi64 tells you that the arguments contain 64-bit signed integers.
Build applications using AVX intrinsics
- Initialize intrinsics. Before you can operate on AVX vectors, you need to fill the vectors with data. Therefore, the first set of intrinsics discussed in this article initialize vectors with data. There are two ways of doing this: initializing vectors with scalar values and initializing vectors with data loaded from memory. The following example creates a 256-bit vector packed with doubles and initializes it with zero.
_m256d vector = _m256_setzero_pd();- Load/store data. Besides creating and initializing a vector, another common usage of AVX is to load data directly from memory into vectors. Then after vector operations, the results are stored back into memory. AVX intrinsics provide a set of functions to load/store data.
- When loading data into vectors, memory alignment becomes particularly important. For each memory load operation, there are two functions. One is for unaligned data whose memory address must be aligned on a 32-byte boundary (that is, the address must be divisible by 32), and another is for unaligned data. An example for loading aligned data:
- float* aligned_floats = (float*)aligned_alloc(32, 64 *
- sizeof(float));
- // some operations
- __m256 aligned_vector = _mm256_load_ps(aligned_floats);
- float* unaligned_floats = (float*)malloc(64 * sizeof(float));
- // some operations
- __m256 unaligend_vector =
- _mm256_loadu_ps(unaligned_floats);
- AVX math operations. Major operations using AVX are math operations. So AVX intrinsics provide users a rich set of math functions, including some basic operations such as addition, subtraction, multiplication, division, permute and shuffle and more complicated ones, such as fuse-multiply-add (FMA) and vector products.
- Compile/build. Before compiling/building the code using AVX intrinsic functions, users should check availability in their development environment, and then add corresponding AVX options to compilers, which indicates intrinsic set including intrinsics used in the code. For example, only if basic AVX intrinsics are used, the code could be compiled by gccas:
gcc -mavx -o <your_avx_code>.cHowever, once FMA is used, the following command should be executed:
gcc -mfma -o <your_avx_code>.cAVX matrix computation example
The following code snippets are from Pronghorn, which is developed in Java but could accelerate matrix operation by C++ AVX function through Java Native Interface (JNI). However, whether it is suitable to use native C/C++ AVX function to optimize Java application needs careful consideration. This is to be explained later.
Baseline Implementation of Integer Vector & Matrix Product Without AVX
- void mulNoAVX(const int row, const int col,
- jint** colSlabs_nat,
- jint* rowSlab_nat,
- const jint rowMask,
- const jlong rowPosition,
- const jint colMask,
- jint* colPositions_nat,
- int* results) {
- for (int c = col - 1; c >= 0; --c) {
- int prod = 0;
- for (int p = row - 1; p >= 0; --p) {
- int v1 = rowSlab_nat[rowMask & (jint)(rowPosition + p)];
- int v2 = colSlabs_nat[c][colMask & (colPositions_nat[c] + p)];
- prod += v1 * v2;
- }
- results[c] = prod;
- }
- }
The pointer rowSlab_nat and colSlabs_nat are a vector and a matrix, respectively. The results of this code is a vector of multiplication of rowSlab_nat and colSlabs_nat. Index operations rowMask & (jint)(rowPosition + p) and colMask & (colPositions_nat[c] + p) calculate the index of the operands of multiplication. In this code, the inner loop actually computes a product of two vectors.
In the implementation with AVX intrinsics, only 256-bit AVX operations are used to improve portability. The code mainly consists of a for loop which has two parts. The first part is the same as the implementation without AVX but only works on the elements that cannot gather into 256-bit vector.
The second part is a loop with multiple AVX operations.
- When loading data the intrinsic function,
_mm256_loadu_si256is responsible for loading unaligned data into a 256-bit vector. Since the input vector and matrix are transferred by JVM through JNI interface, it is impossible to control the alignment of the data. Although in a normal case, load/store unaligned data could bring extra overhead, modern processors optimized the behavior of load/store instruction and reduced the difference of performance between aligned and unaligned data. - If the vector may be used to store different data types,
_mm256_cvtepi32_psand other conversion intrinsic functions can convert the data in the vector to correct data type. - The operation of dot product of two vectors is a little bit complicated. The result vector stores a half of the result of product into the first byte and the other half into the 5th byte. Like this, there are some intrinsic in AVX math operations are not executed in an intuitive way. Users should refer to the document and check usages of them carefully.
- The AVX operation applies loop transformations like loop stripmine/fission to help vectorization. It also applies the technique of loop unrolling to improve the opportunity of the processor to exploit out-of-order instruction execution.
AVX Implementation of Vector and Matrix
- void mulAVXInt(const int row, const int col,
- jint** colSlabs_nat,
- jint* rowSlab_nat,
- const jint rowMask,
- const jlong rowPosition,
- const jint colMask,
- jint* colPositions_nat,
- int* results) {
- __m256 ymm0, ymm1, ymm2, ymm3, ymm4, ymm5, ymm6;
- for (int c = col - 1; c >= 0; --c) {
- int prod = 0;
- int row_remain = (row - 1) - (row - 1)%16;
- for (int p = (row - 1); p >= row_remain; --p) {
- int v1 = rowSlab_nat[rowMask & (jint)(rowPosition + p)];
- int v2 = colSlabs_nat[c][colMask & (colPositions_nat[c] + p)];
- prod += v1 * v2;
- }
-
- // upgrade integer to float due to no dot product for int of AVX
- // another implementation is to use "hadd" instructions
- // see example (http://stackoverflow.com/questions/23186348/integer-dot-product-using-sse-avx?rq=1)
- for (int p = row_remain - 1; p >= 0; p -= 16) {
- ymm0 = _mm256_cvtepi32_ps(_mm256_loadu_si256((__m256i *)(&rowSlab_nat[(int)rowMask & ((int)(rowPosition) + p - 7)])));
- ymm1 = _mm256_cvtepi32_ps(_mm256_loadu_si256((__m256i *)(&rowSlab_nat[(int)rowMask & ((int)(rowPosition) + p - 15)])));
- ymm2 = _mm256_cvtepi32_ps(_mm256_loadu_si256((__m256i *)&colSlabs_nat[c][colMask & (colPositions_nat[c] + p - 7)]));
- ymm3 = _mm256_cvtepi32_ps(_mm256_loadu_si256((__m256i *)&colSlabs_nat[c][colMask & (colPositions_nat[c] + p - 15)]));
-
- ymm4 = _mm256_dp_ps(ymm0, ymm2, 255);
- ymm5 = _mm256_dp_ps(ymm1, ymm3, 255);
- ymm6 = _mm256_add_ps(ymm4, ymm5);
- float tmp_prod[8] = {0};
- _mm256_storeu_ps(tmp_prod, ymm6);
- prod += (int)tmp_prod[0] + (int)tmp_prod[4];
- }
- // results[c] = prod;
- memcpy((void*)(results + c), (void*)&prod, sizeof(int));
- }
- }
-
Vectorization in other languages
Although aforementioned, vectorization through AVX is only shown using C/C++ code for convenience. In other languages, it is also possible to take advantage of AVX optimization.
Java
Since Java application is running on JVM, there is no direct usage of AVX optimization in Java. However, we still could leverage JIT for automatic vectorization, or further AVX optimization through JNI.
- The hotspot JVM implements automatic vectorization in version 8. Specifically, the Hotspot compiler implements the concept of the Superword Level Parallelism Hotspot JVM option. Specifically, JVM could use the option
-XX:+UseSuperWordto enable automatic vectorization. However, the JIT compiler suffers from two main disadvantages. First, the JIT is a black box for developers. There is no control on optimization phases like vectorization. Secondly, the time constraint narrows down the degree of optimization compared to static compilers like GCC or LLVM. So, it is compelling to use statically compiled code since it benefits from additional optimization reducing performance bottlenecks. Static compilation can be achieved through JNI in Java. - JNI is a specification which allows applications to call statically compiled methods from dynamic libraries and to manipulate Java objects from there. So through JNI we can realize all AVX optimization aforementioned. But normally JNI suffers from an additional invocation cost. Invoking a native target function requires two calls. The first is from the Java application to the JNI wrapper which sets up the native function parameters. The second is from the JNI wrapper to the native target function. The most significant source of overhead occurs during the invocation of JNI callbacks. An example is to get an array pointer from the Java heap. A callback pays a performance penalty because two levels of indirection are used: one to obtain the appropriate function pointer inside a function table, and one to invoke the function. Yet, these callbacks remain necessary to work with Java objects while avoiding memory copies that are even more expensive. In addition to the Java heap, where objects are allocated and automatically removed by the garbage collector, Java allows programmers to allocate chunks of memory out of the Java heap. This kind of memory is called native memory. But JNI specification does not recommend the use of native memory directly since it cause instability of JVM and other issues.
Comparison of JIT and JNI Vectorization
| Drawbacks | Benefits | |
|---|---|---|
| JIT | no control of optimization | lower overhead |
| JNI | Customized optimization | higher overhead |
Python
The python library, Numpy, has optimized its code to leverage AVX/AVX2. Since it is a cornerstone of most application involved math and matrix operations, there is no need for users to do manual optimization. But vectorization at the level of python code may still be useful since it allows Numpy to implement the operations based on vectorization at the machine level using AVX.
Conclusion
This article only examines basic ideas and usages of vectorization for performance optimization. A simple example demonstrates the process of using AVX intrinsics implement vectorization.
As a powerful performance optimization technique, vectorization could be applied in many applications, especially considering the rich instruction set support of SIMD in mainstream modern processor architectures. Although manual vectorization could require some effort and careful thought on algorithm and implementation, in some cases, it may achieve greater speedup than automatic vectorization generated by compilers.
Acknowledgements
This article is inspired by optimizing math performance for a Pronghorn project at OCI. I want to thank my colleagues Adam Mitz, Nathan Tippy, and Charles Calkins from OCI for their useful and professional comments that greatly improved the quality of this article.
Futher Reading
- Intel AVX Intrinsics Guide for AVX, definition of specific intrinsics.
- GCC options, include AVX related option.
- Optimizing Compilers for Modern Architectures: A Dependence-based Approach, a text book including many loop transformation and vectorization techniques.
- Automatic vectorization, wiki about techniques used for automatic vectorization but it is also useful for manual vectorization.
- Intel Xeon Phi Processor High Performance Programming, 2nd Edition Knights Landing Edition, a guide of performance optimization on Xeon Phi architecture, including but not limiting on vectorization.
Software Engineering Tech Trends (SETT) is a regular publication featuring emerging trends in software engineering.
